I den förra faktarutan byggde optimeringen på att vi fördelade de relativa vinkel-felen så att de var lika stora till sina belopp vid R(1), R(2) och R(min). Den situationen hittar vi när offset-vinkeln sätts till β(optimal).

Som vi kan se av ekvation 8 är R(min) omvänt proportionell mot β. Det innebär att om offset-vinkeln är större än β(optimal) kommer R(min) att vara mindre än R(optimal) – och tvärt om. Därför behöver vi genomföra optimeringen på olika sätt för dessa båda fall.

Baerwald, som baserar sin härledning på en Tchebychev-approximation, redovisar därför följande indelning för bästa resultat:


Här finns en, vid mindre vinklar två, nollradier. Distorsionen är störst längst in på skivan, varför vi försöker minimera m(1).


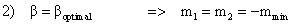
Detta är optimum enligt vår ekvation [3].


Här finns endast en nollradie. Distorsionen är störst längst ut på skivan, varför vi försöker minimera m(2).

Dessvärre finns det ytterligare en komplikation. Vid offset-vinklar som är så små att R(min) blir mindre än R(1) tappar m(min) värde för oss. Därför behöver vi titta särskilt på den situation där R(min) = R(1). Den offset-vinkel som gäller precis då kallar Baerwald för ”kritisk”, så låt oss kalla den β(kritisk).

Den tredje punkten behöver således ändras till


Här finns endast en nollradie. Distorsionen är störst längst ut på skivan, varför vi försöker minimera m(2).

När β är mindre än β(kritisk) vi behöver byta metodik ännu en gång, och försöker i stället balansera m(1) = m(2) för minsta relativa vinkelfel.


Även här finns endast en nollradie.

Nu kan vi härleda uttrycken för bästa värdet på C för dessa fyra olika situationer. Den andra situationen har vi ju redan klarat av (i förra faktarutan) så den lämnar vi därhän. För att kunna bedöma vilken situation vi faktiskt har, behöver vi veta det exakta värdet på vår offset-vinkel, men vi måste också beräkna vinklarna β(optimal) och β(kritisk).

β(optimal) beräknar vi med hjälp av ekvation [11] eller [11a]. β(kritisk) beräknar vi som den offset-vinkel som ger R(min) = R(1):

Vi söker det värde på C som ger oss m(1) = –m(min). Ekvationerna [5] och [9] ger oss m(1) respektive m(min). Vi sätter samman ekvationerna [5] och [9] och utvecklar:



Vi löser ut C:







Det här är en andragradsekvation i

som har lösningen



Ur denna ekvation löser vi C:

Vi söker det värde på C som ger oss m(2) = –m(min). Denna härledning blir exakt densamma som den förra, bortsett från att R(1) byts ut mot R(2). Därför kan vi teckna bästa C för detta fall:

Vi söker det värde på C som ger oss m(2) = –m(1). Ekvationerna [5] och [6] ger oss m(1) respektive m(2). Vi sätter samman ekvationerna [5] och [6] och utvecklar:









Så, nu har vi alla samband för den bästa inställningen även för de tonarmar som har fast längd och fast offset-vinkel.

För varje värde på L och β kan vi nu beräkna de optimala värdena på C med hjälp av ekvationerna [13], [14] respektive [15]. Som vi kan se är C parametrarna beroende av både L och β samt radierna för skivans inner- och ytterspår.

Om vi sätter in de värden innerradien (61,0 mm) och ytterradien (145 mm) vi använt tidigare, kan vi förenkla ekvationerna på följande (sätt in L i mm och β i grader):













De här ekvationerna motsvarar de värden jag visade i tabellen med inställningar av bästa C. (Vid en jämförelse kan det skilja något på grund avrundningsfenomen).

Observera att jag i tabellen redan valt mellan de olika situationerna, varför tabellen går att avända rakt av som den är, oavsett värdet på β.

Sida 1 Sida 2 Sida 3 Sida 4 Sida 5 Sida 6 Sida7 Sida 8 Sida 9
 
 © HiFiForum.nu except: Logos and Trademarks are property of their owners. All Rights Reserved